1 题目介绍
本题的大意就是在一个序列 中,求删去若干个数字,使得剩下的数字是等差数列得方法数,从动态规划的角度,这是标准的计数类 DP。
最后的数据也告诉我们时间复杂度是 {} 或 大约 {} 的。
2 解析
2.1 开端
猎奇解法的开端:勇于尝试
对于等差数列,最显著的特征就是公差相等。我的想法是首先计算出任意两个数字的差(显然是平方复杂度),再研究有什么 好 算 法 。
假设 表示 ,对于样例 的数据(注:后文所有的举例推导都是来自样例 的数据):
8
13 14 6 20 27 34 34 41
手算(也可以电脑算)很容易得出这样的关于 数组的表:
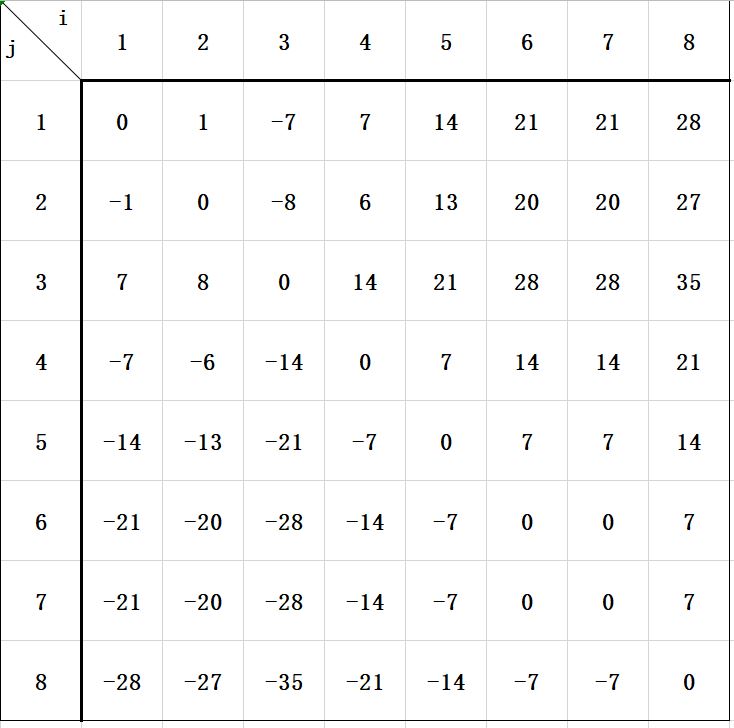
在这个表里面,找到了两个特点:
- 该表的左上到右下的对角线格子(即所有 )都是 ;
- 以该线为对称轴,对称的两个格子的数互为相反数。
主要利用的是第二个特点,这样子就没有必要求出整个 数组,只需要求一半(这里选择哪一半形都行,这里我选择右上的这一半)。
其次还是利用第一个特点,这样子就不需要存储一个对角线的 了,那么在我存储的内容中,对于坐标 ,一定有 。
2.2 核心算法
既然等差数列的公差相等,也就是说在这个 数组里面,数值一样的几个地方可以作为等差数列的一部分。
这句话非常不好理解,我举个例子好了: 和 可以作为等差数列,还原到输入的 数组里面,对应的就是 三个数。同样第五行的两个 也可以进来,但是注意同一行的多个可行方案(公差不是 )只能选择入一个,这是为什么呢?
假设你把 和 两个都并进去了,还原到原来的 数组,那么你留下的数字就是 ,很明显这不是等差数列。
说得逻辑化一点,因为同一行的数字其实是不同的 减去了一个相同的 ,之所以数字一样,就是因为这几个 都一样,除非你的等差数列都是同一个数,这是不合法的。
我貌似没有特判公差非 也对了
那么选择 ,, 可不可以呢?遇事不决,暴力还原。选择这两个数字,意味着你的 数组选择了 ,这也很明显不是等差数列,如果加上 ,它就是完整的等差数列了。
对应一下,也就是说要加上 ,发现什么规律了吗?
按从上到下的顺序选择相等的公差时,保证“坐标的连续性”,也就是说,假若选择 ,一定有对于所有的 ,。
这又是为何呢?因为 表示的是 ,所以一定要保证“坐标连续性”,后一个的 才能等于前一个的 ,它才是一个完美无缺的等差数列。
那么就是说, 对应的相等的数只能在第四行找, 对应的相等的数只能在第五行找, 对应的相等的数只能在第 行找……
然后就有了下面的关系:
(这里的 单纯是或者的意思没有位运算或其他意思)
是不是觉得这个关系可以……
建一个 DAG ?
姑且只对这个样例建的图进行分析,那么在 里找等差数列这个问题,不就转换成找这个图里有几条路径(最后再加上节点个数)吗?
进一步分析全局,对于每一个不同的公差,都会有一个这样子的图,也就是说,对于每一个公差(也就是每一个图),都求解一遍 这个图里有几条路径 这个问题就好了。
关于一个图内部有几条路径,很明显的搜索或 DP 吧?
不过既然是在图上 DP,还是打搜索(或记忆搜)比较容易防止出现奇奇怪怪的细节 bug。
void dfs(int u){// u表示现在搜到哪个节点
if(vis[u]) return; // 如果已经走过了,回溯
vis[u]=dp[u]=1; // 标记这个点已经走过,对dp赋初值
for(register int i=0;i<l[u].size();++i){
/*用邻接矩阵存图,l[i]表示i号点连向的所有点
*注意这里不可以写 if(vis[l[u][i]) continue;
*因为无论搜不搜都需要更新dp[u]的值
*/
dfs(l[u][i]),
dp[u]+=dp[l[u][i]],
dp[u]%=mod; // 一定不要忘记取模
}
s+=dp[u],s%=mod; // s存储答案
return;
}
这里有人质疑了:如何保证这个图是 DAG ?如果要 DP ,是不是还要先拓扑排序?
如何保证图是 DAG ?
很显然,因为对于一个三角形内,坐标 所连向的点一定在三角形下方,而如果三角形下方的点要连回上方,则 ,但是对于我的存储方法(右上角为直角的直角三角形存储,见前文,一定要 ),倘若 ,那么这个点根本不在三角形内,也就是无论怎样都不会连上去。
同理,如果你选择的是左下的三角形的存储,那么要从下面跳到上面,一定要有 ,满足 ,但是对于这种存储方法,一定有 ,所以也不必担心。
图是个 DAG,并不是用其他的特判来保证的,而是它本来就一定是 DAG。
DP 或搜索需不需要先拓扑排序?
按照上述的方法建图,不难想到,一定会有后面的点所在行比前面的点所在行要大。也就是行数一定是递增的(在任意一条路径上,行数是严格递增的),本身不存在后效性。
而这个图本身的拓扑序也一定是 递增的,所以不需要拓扑排序。
对于其他问题,请评论提问,基本我有空就会回答。
2.4 失误与特判
这个代码我交了很多遍,总是有一个数据点 MLE,但是理论上 MLE 的现象基本不会出现,我尝试进行空间优化,依旧是 其他数据跑得很快,唯独一个 MLE。 我仔细思考了可能的原因,发现了代码缺陷。
一个非正解而且如此猎奇的代码固然是有缺陷的。那就是对于本身所有数字都相等,又因为我的建图方式是邻接表,这种方式会造成很大的空间浪费。
对于这类无法解决的 分,我采用的是最无脑的方法——特判。
假设输入 数组全部相等,经过手算可以得知,设总共 个数,则有 种方法。注意此时不能直接用 pow 函数,要快速幂方便取模。
2.5 复杂度分析
对于构造 数组,很明显的 。
对于建图,这是个很悬的问题,理论复杂度是 ,因为对于每个点,都需要扫描一整行来寻找有没有和它相等的点。但是因为各种常数优化(比如本身只存了半个 数组)和玄学东西,导致它复杂度比期望值小得多得多。(关于这一段的复杂度,我和机房其他神佬也没有研究明白,如果有研究明白了的,请私信我,谢谢)
对于跑图,因为每一个公差都会造一个图,这些图总共的点数是 ,搜索时每个点只会到一次,所以这一段复杂度也是 。
3. 代码
注:各位既然都在做这道蓝题了,非常简单的代码部分注释不会很详细的,而且谁闲着无聊给输入输出之类的都打上注释啊。
#include<vector>
#include<cstdio>
#define mod 998244353
int n,t,s,a[1001],c[1001][1001],id[1001][1001],dp[500001];
bool vis[500001],tp=1;
std::vector<int> l[500001]; // 邻接表存图
void dfs(int u){// 搜索,前面已经展示过详细注释了
if(vis[u]) return;
vis[u]=dp[u]=1;
for(register int i=0;i<l[u].size();++i){
dfs(l[u][i]);
dp[u]+=dp[l[u][i]],dp[u]%=mod;
}
s+=dp[u],s%=mod;
return;
}
inline long long pw(long long a,long long b){// 快速幂
long long s=1,t=a;
while(b>0){
if(b&1) s*=t,s%=mod;
b>>=1, t*=t,t%=mod;
}
return s;
}
int main(){
scanf("%d",&n);
s=n; // 千万不要忘记了单个点也是等差数列
for(register int i=1;i<=n;++i){
scanf("%d",&a[i]);
if(i>1 && a[i]!=a[i-1]) tp=0; // 特判:是不是所有数字相等
}
if(tp){ // 特判:如果是,直接快速幂
printf("%lld",pw(2,n)-1);
return 0;
}
for(register int i=1;i<n;++i) for(register int j=i+1;j<=n;++j){
//printf(""); 这是个玄学的地方,没有它程序有几率炸掉,读代码时不必理会
id[i][j]=++t; // 给每个点记一个编号方便建图
c[i][j]=a[i]-a[j];
}
for(register int i=1;i<n;++i)
for(register int j=i+1;j<=n;++j)
for(register int k=j+1;k<=n;++k)
// 第1、2层循环枚举每一个点(i,j),第2、3层循环枚举与之对应的相等的点(j,k)
if(c[i][j]==c[j][k])
l[id[i][j]].push_back(id[j][k]);// 邻接表式建边
for(register int i=1;i<=t;++i) if(!vis[i]) dfs(i);
// 每个图之间不连通,不能直接dfs(1);
printf("%d",s);
return 0;
}
